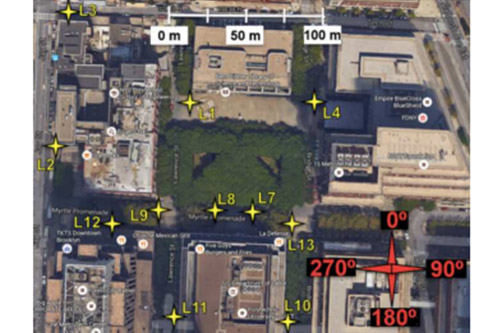
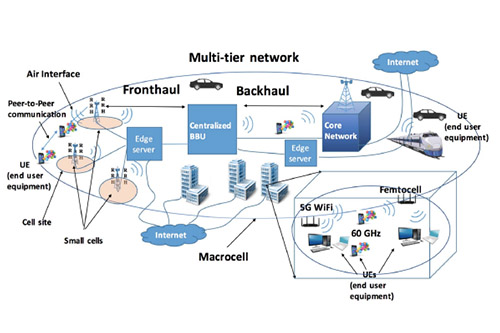
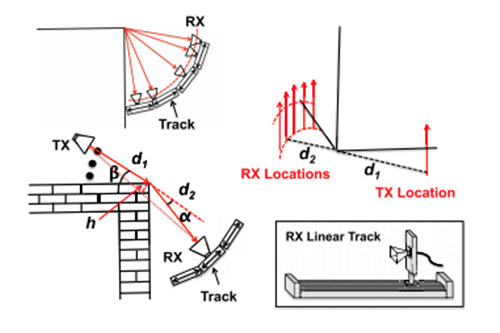
Thomas Marzetta
DIRECTOR NYU WIRELESS
Distinguished Industry Professor
| Phone: | 646.997.3028 |
| Email: | tlm8@nyu.edu |
| Office: | 370 Jay Street, 9th Fl, Brooklyn, NY 11201 |

-
about
Thomas Marzetta is Distinguished Industry Professor at NYU Tandon School of Engineering’s Electrical and Computer Engineering Department and an Associate Director of NYU WIRELESS. Born in Washington, D.C., he received the Ph.D. and SB in Electrical Engineering from Massachusetts Institute of Technology in 1978 and 1972, and the MS in Systems Engineering from University of Pennsylvania in 1973. Prior to joining NYU in 2017, he had three industrial research careers: petroleum exploration (Schlumberger-Doll Research, 1978 – 1987), defense (Nichols Research Corporation, 1987 – 1995), and telecommunications (Bell Labs, 1995 – 2017). At Bell Labs, he directed the Communications and Statistical Sciences Department within the former Mathematical Sciences Research Center, and he was elected a Bell Labs Fellow. He originated Massive MIMO, one of the cornerstones of fifth-generation wireless technology. He is lead author of the book Fundamentals of Massive MIMO.
Professor Marzetta was on the Advisory Board of MAMMOET (Massive MIMO for Efficient Transmission), an EU-sponsored FP7 project, and he was Coordinator of the GreenTouch Consortium’s Large Scale Antenna Systems Project. Recognition for his contributions to Massive MIMO include the 2017 IEEE Communications Society Industrial Innovation Award, the 2015 IEEE Stephen O. Rice Prize, and the 2015 IEEE W. R. G. Baker Award. He was elected a Fellow of the IEEE in 2003, and he received an Honorary Doctorate from Linköping University in 2015.
Research Interests: Massive MIMO (Multiple-Input Multiple-Output), Wireless technology
-
lecture series
“A Linear System Theory Approach to Wave Propagation”
The premise of this lecture series is that the traditional physicist’s approach to teaching electromagnetic theory – which entails scalar and vector potentials, the method of separation of variables, spherical coordinates, and the frequent use of special functions – obscures some of its most important implications. Instead, we treat Maxwell’s equations as descriptive of a linear space/time-invariant system, amenable to tools of linear system theory that are familiar to signal processing engineers and communication theorists: convolutions and space/time Fourier transforms, performed in space/time Cartesian coordinates.
Rather than starting with electromagnetic wave propagation, instead, we begin with acoustic wave propagation. There are good reasons for this. First, the acoustic field is a scalar field, whereas the electromagnetic field is a vector field. Hence, the notation for the acoustic field is less cluttered than for the electromagnetic field. Second, the physics of the acoustic field is simpler than that of the electromagnetic field, and more intuitive. Third, with the exception of polarization, all of the wave propagation phenomenology associated with electromagnetics is manifested in acoustics.
The required background is linear system theory, comfort with convolutions and Fourier transforms, and familiarity with functions of complex variables.
This lecture series will benefit both signal processing researchers and communication theorists. It will equip them to understand advanced topics, such as wave equation migration filtering, wireless power transfer via evanescent wave coupling, super-directive antenna arrays, large intelligent surfaces, and holographic MIMO.
Outline
Lecture 1
- Systems of antennas and circuit theory
- Impedance matrix
- Real and reactive power
- Fundamentals of wireless power transfer
- Wireless power transfer efficiency
Lecture 2
- Introduction to acoustics
- pressure/strain relation
- distributed source
- Newton’s second law
- 3D wave equation for pressure, resulting from a distributed source
- 1D wave propagation
- 1D plane-waves
- Helmholtz equation with distributed source
- solution of Helmholtz equation for the pressure field via Green’s function
Lecture 3
- 1D wave propagation (continued)
- solution of Helmholtz equation is spatial frequency domain
- review of Cauchy integral & residue theorems
- inverse spatial Fourier transform via residues
- source of limited extent: pressure field inside the source vs. outside the source
- computation of power
- self-impedance of source
- mutual impedance between two sources
- solution of Helmholtz equation is spatial frequency domain
Lecture 4
- Solution of 3D Helmholtz equation for pressure in spatial Fourier domain
- residues, and the plane-wave representation of pressure field
- ordinary plane waves and evanescent plane waves
- Plane-wave representation of spherical wave
- Greene’s function representation for pressure field
Lecture 5
- Pressure field: inside distributed source vs. outside
- Degrees of freedom associated with an array of sources
- Real power and conservation of energy
Lecture 6
- Equivalent ways of computing power
- Direct integration over distributed source
- Power carried by propagating plane-waves
- Far-field power
Lecture 7
- Self-impedance of distributed source
- Mutual impedance between two distributed sources
- Physically realistic source models
Lecture 8
- Review of Maxwell’s equations with distributed electric/magnetic current sources
- Direct solution of Maxwell’s equations in space/time Fourier domain for E and H fields
- Residues, and the plane-wave representation of the electromagnetic field
Lecture 9
- Power: real and reactive
- Poynting vector
Lecture 10
- Electromagnetic sources
- Self-impedance and mutual impedance
- Systems of antennas and circuit theory
EDUCATION
University of Pennsylvania, 1973
Master of Science, Systems Engineering
Massachusetts Institute of Technology, 1978
Doctor of Philosophy, Electrical Engineering
Massachusetts Institute of Technology, 1972
Bachelor of Science, Electrical Engineering

 2025 Brooklyn 6G Summit — November 5-7
2025 Brooklyn 6G Summit — November 5-7 Sundeep Rangan & Team Receive NTIA Award
Sundeep Rangan & Team Receive NTIA Award 2025 Open House
2025 Open House