The increasing prevalence of distributed sensing and communication networks, from camera arrays to large-scale IoT systems, has created a need for efficient data compression methods that exploit inter-source correlations. While classical information theory provides fundamental limits for such distributed settings, practical algorithms that achieve these limits remain elusive. This research develops learning-based, interpretable frameworks for distributed compression and communication that adhere to information-theoretic principles while remaining scalable and practical.

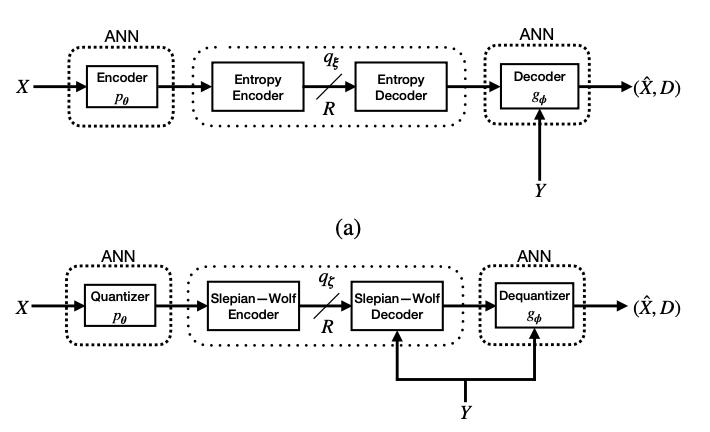
LEARNING-BASED WYNER–ZIV COMPRESSION

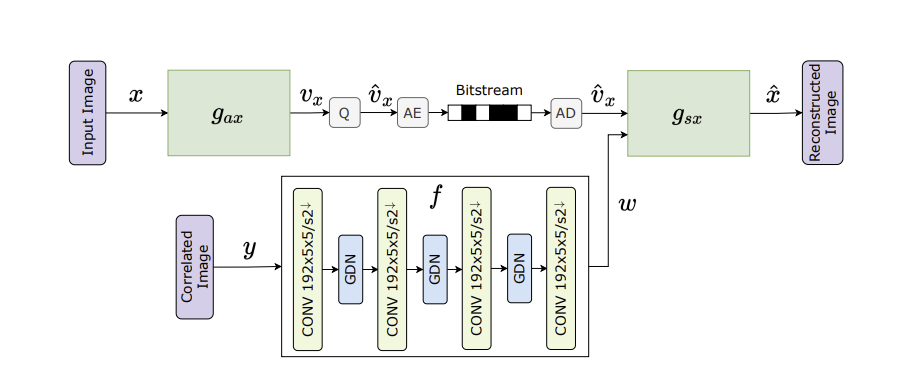
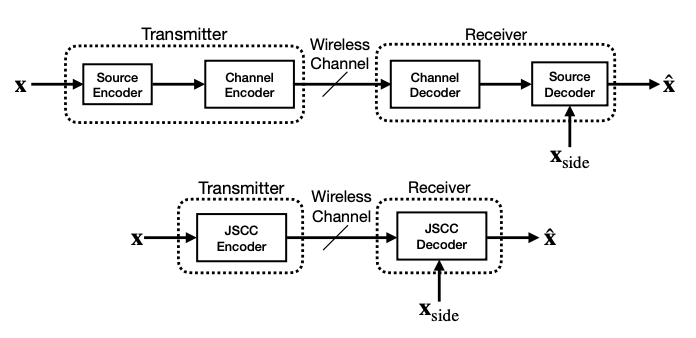
A key line of work focuses on the Wyner–Ziv problem [1], which addresses compression with side information available only at the decoder. Traditional methods often rely on strong assumptions about source statistics, limiting real-world applicability. The proposed learning-based compressors [2], [3] overcome this by learning essential characteristics of the theoretically optimal solution directly from data. This allows recovery of information-theoretic binning in a data driven manner. Unlike existing stateof-the-art neural transform coding-based schemes [4], the approach efficiently exploits side information, approaching theoretical rate–distortion bounds and offering interpretability by revealing how networks internalize core information-theoretic behavior.
This project was supported by the Google Research Collabs Program.

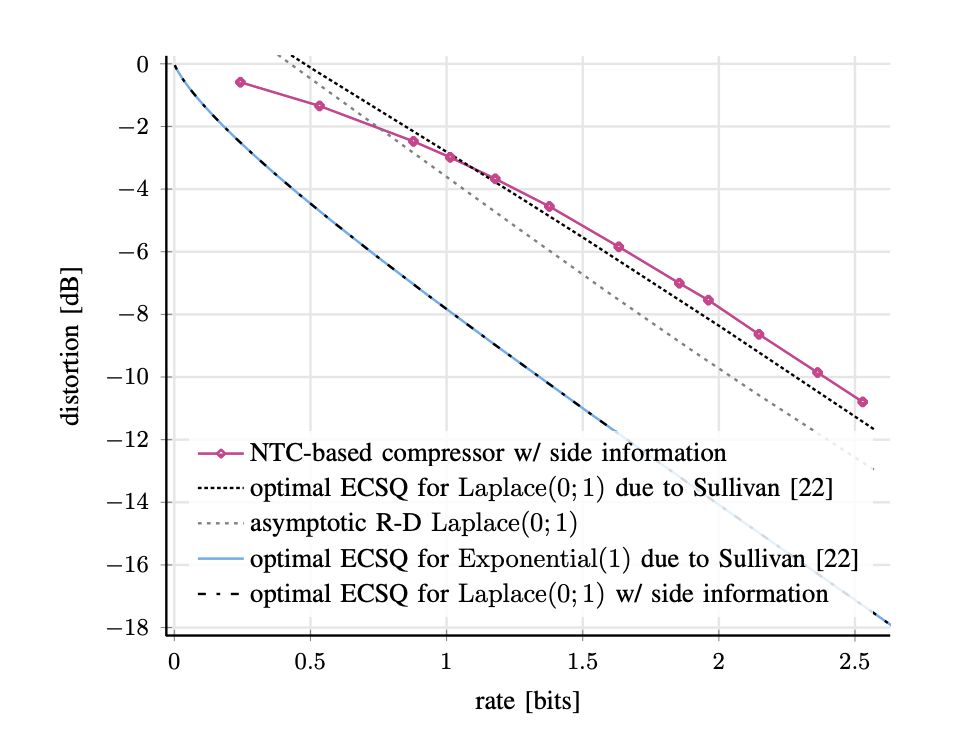
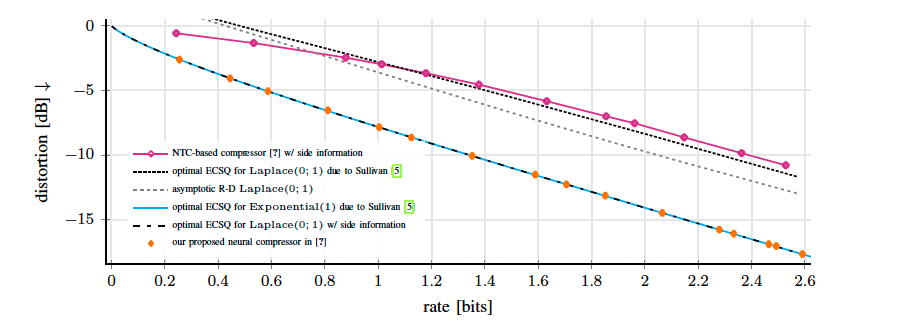
Fig. 1: Rate–distortion performances (R-D) obtained with Nonlinear Transform Coding (NTC) [4], which is adapted to incorporate the available side information as the objective function. We consider a simple one-shot source coding with side information setup: let X ∼ Laplace(0; 1) and Y = sgn(X), i.e., the sign function of the input realization, and let the distortion metric d(·, ·) be mean-squared error. Unlike the class of state-of-the-art methods, termed NTC, our proposed formulation in [3] recovers the theoretically optimum R-D function with side information.

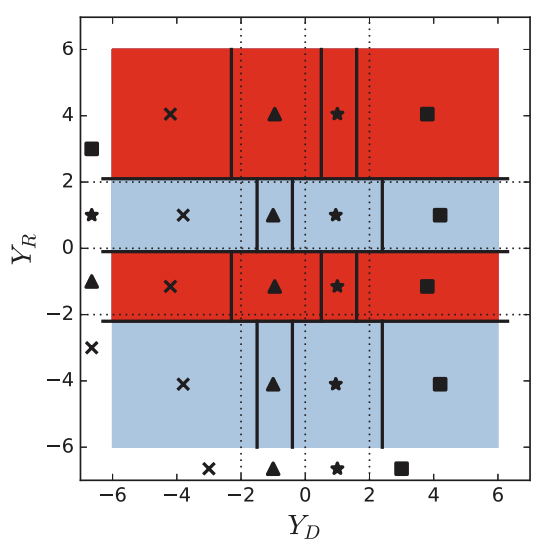
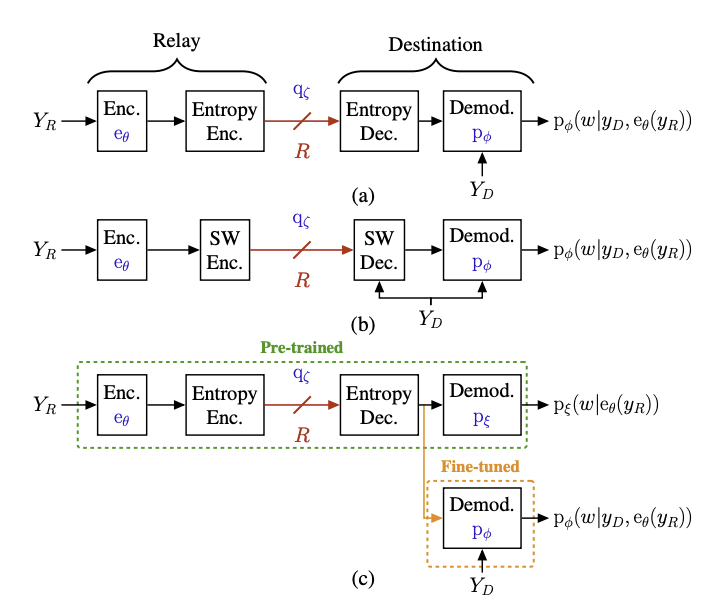
LEARNING-BASED COMPRESS-AND-FORWARD COMMUNICATION

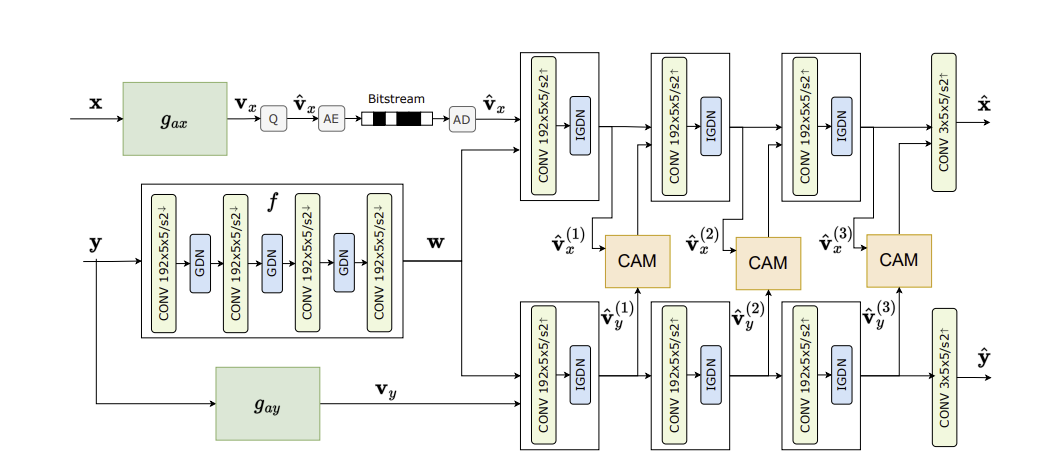
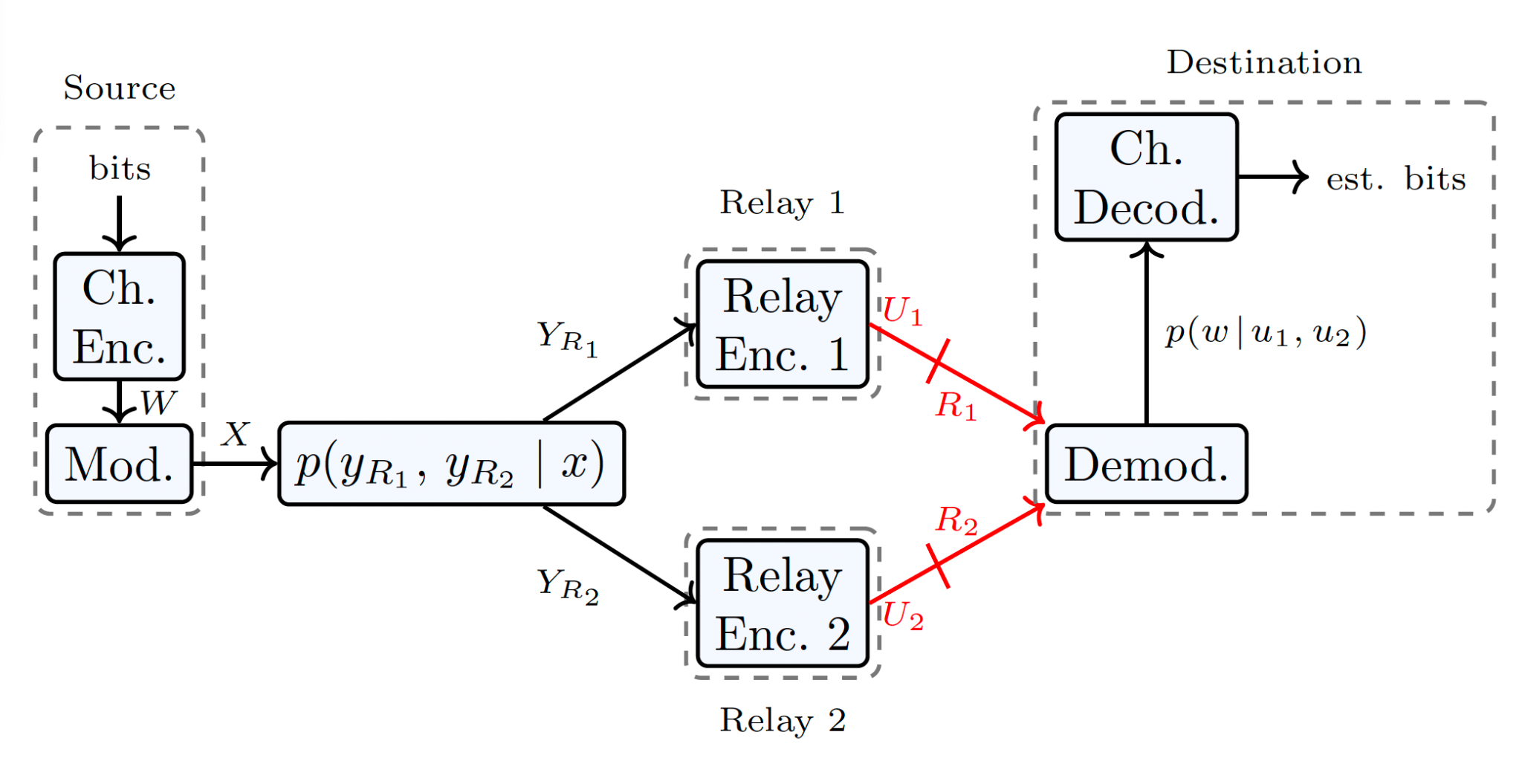
Building on insights from distributed compression, this work extends to cooperative communication, specifically the compress-and-forward (CF) relaying strategy. In this setting, relay nodes compress and forward their received signals while exploiting inter-signal correlations at the receiver. The proposed learning-based CF methods [6], [7] recover solutions close to the theoretical optimum and significantly improve spectral efficiency and throughput—key requirements for 6G systems.

BROADER IMPACT

These findings have broader implications for edge inference, federated learning, and multi-view image/video compression [8], [9]. Recent contributions [10]–[14] continue integrating information theory and deep learning, paving the way for next generation distributed compression and communication systems that bridge theory and practice.

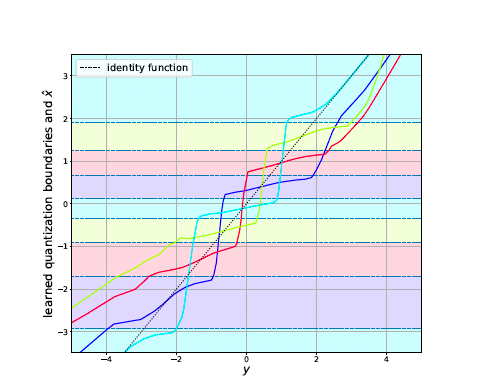
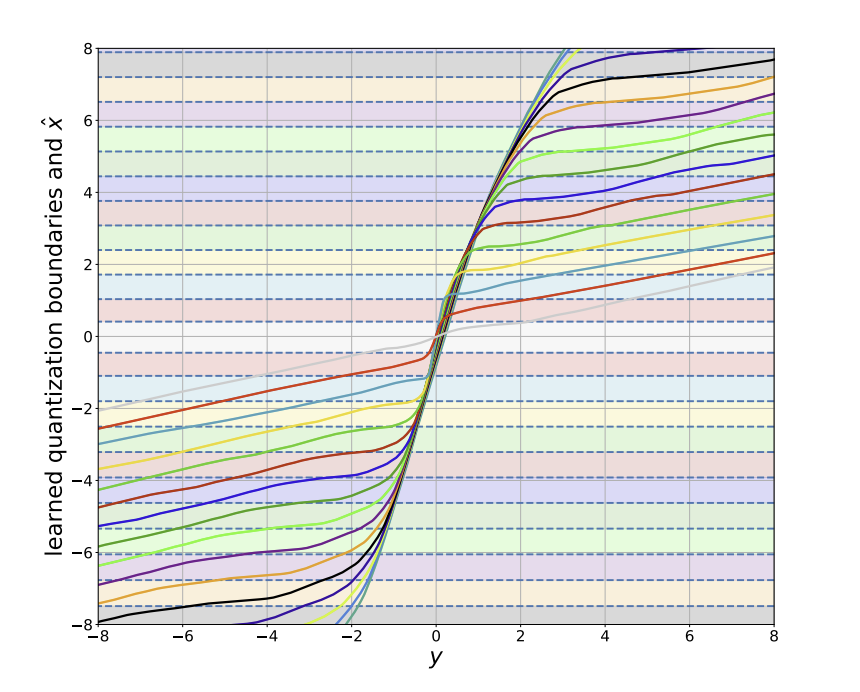
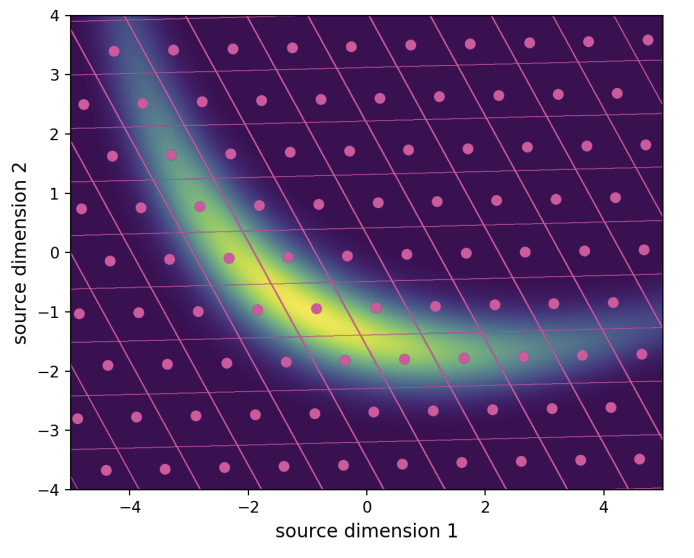
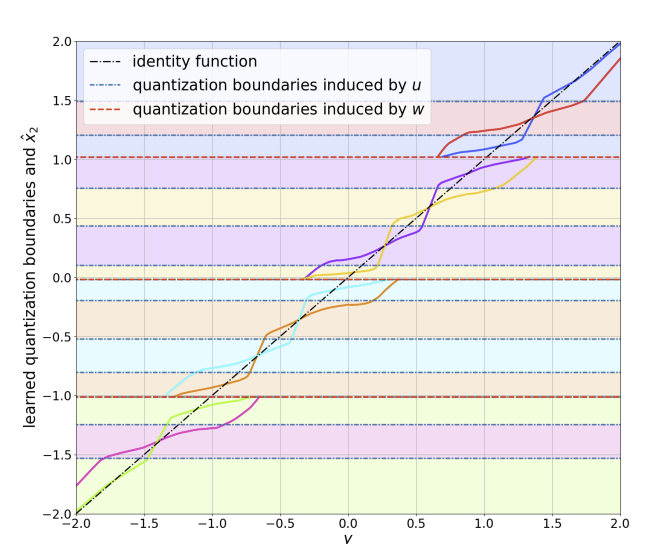
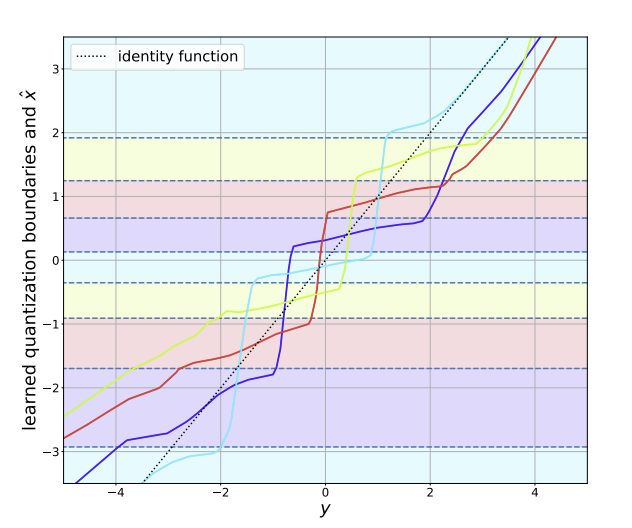
Fig. 2: Figure taken from [2]. Visualization (best viewed in color) of the learned encoder and decoder of the operational scheme proposed in [2], for the quadratic-Gaussian Wyner–Ziv setup. The dashed horizontal lines are quantization boundaries, and the colors between boundaries represent unique values of bin indices. The decoding function is depicted as separate plots for each value of bin index, using the same color assignment. Color coding reveals that our proposed model learns discontiguous quantization bins.