The relay channel, consisting of a source-destination pair along with a relay, is a fundamental component of cooperative communications, given in Fig. 1. While the capacity of a general relay channel remains unknown, various relaying strategies, including compress-and-forward (CF), have been proposed. In CF, the relay forwards a quantized version of its received signal to the destination. Given the correlated signals at the relay and destination, distributed compression techniques, such as Wyner-Ziv coding, can be harnessed to utilize the relay-to-destination link more efficiently. Leveraging recent advances in neural network-based distributed compression, we revisit the relay channel problem and integrate a learned task-aware Wyner-Ziv compressor into a primitive relay channel with a finite-capacity out-of-band relay-to-destination link. The proposed neural CF, employing finite order modulation, operates closely to the rate achievable in a primitive relay channel with a Gaussian codebook and provides interpretable compression/decompression techniques in Fig. 2, and visualized in Fig. 3 [1,2].

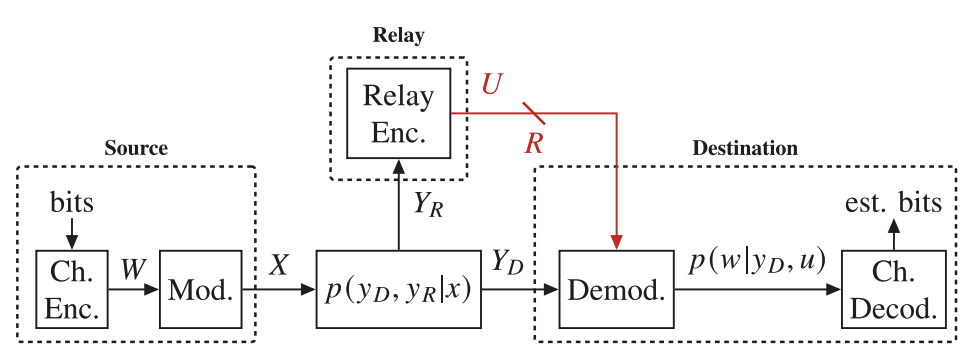
Fig. 1: The primitive relay channel (PRC) under consideration. The red link denotes out-of-band relaying between the relay and the destination.

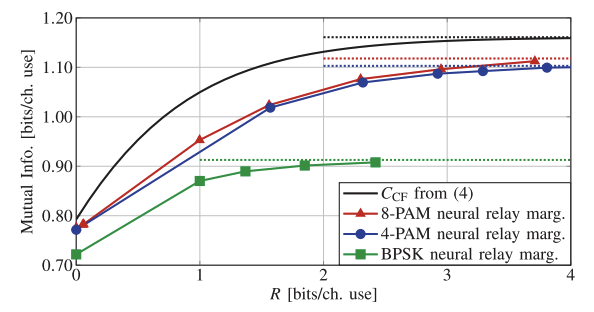
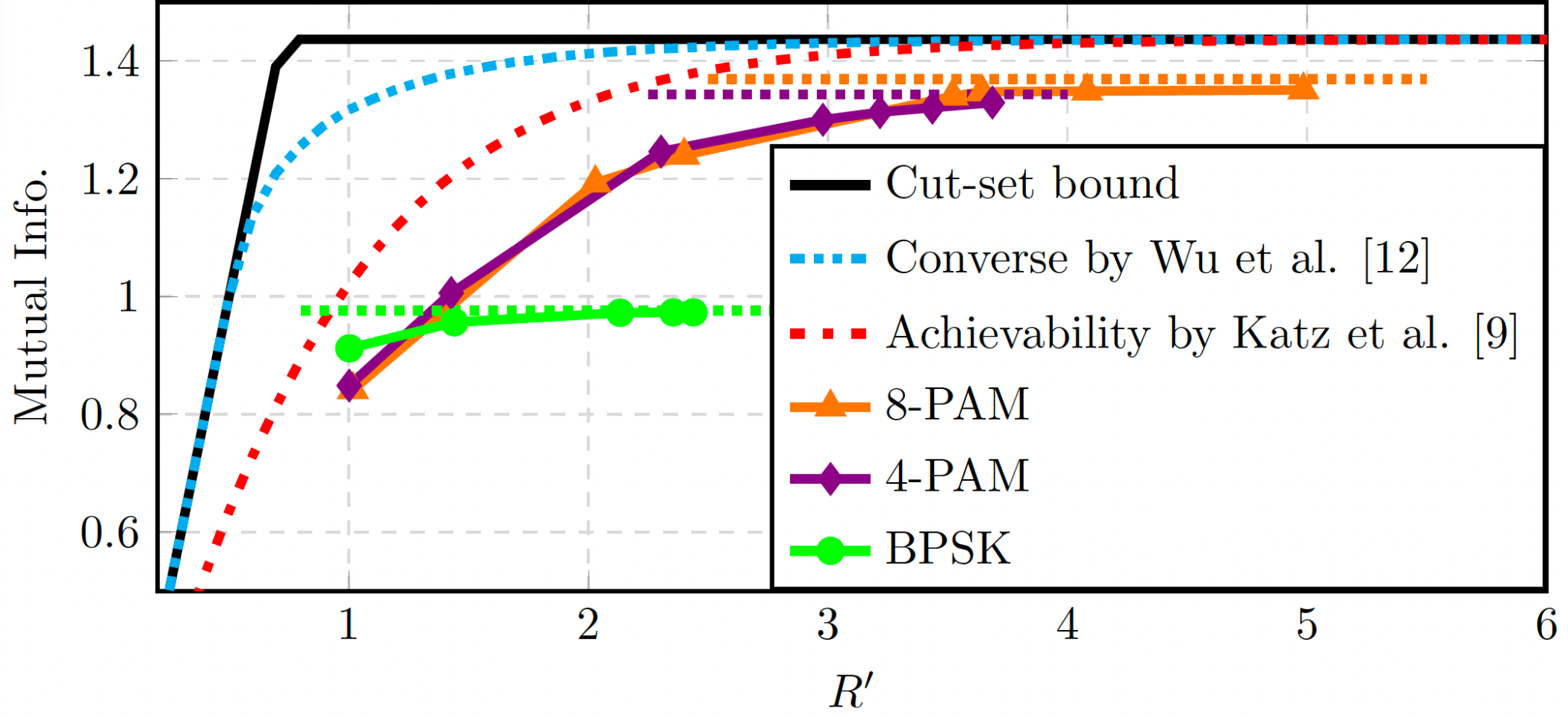
Fig. 2: Mutual information for the CF on the relay channel in case of BPSK, 4-PAM and 8-PAM modulations with γD = γR = 3 dB. The solid line represents the cutset bound, obtained for Gaussian inputs. The dotted lines represent the perfect relay (R → ∞) bounds for the respective curves.

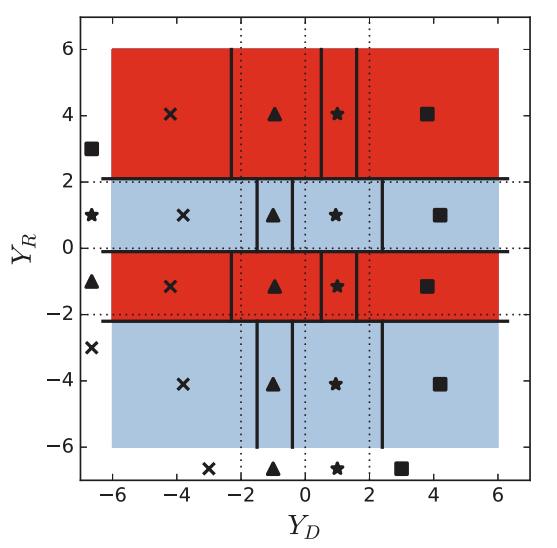
Fig. 3: Visualization (best viewed in color) of the learned CF strategy and demodulation decisions for the 4-PAM modulation with γ = 13 and relay rate R ≈ 1. The horizontal lines denote the quantization boundaries on YR, and the colors designate the transmitted index. The vertical lines denote the hard decision boundaries for the demodulator, and the markers represent the decisions. The transmitted symbols (denoted by cross, triangle, star, square) are also reported near the axis for reference.

We also extend the idea of learned CF onto the diamond relay channel, where a source communicates with a destination via two parallel relays, modeling distributed processing in cloud RAN, illustrated in Fig. 4. We focus on the primitive variant, where each relay observes a noisy version of the source signal and forwards a compressed description over an orthogonal, noiseless, finite-rate link to the destination. We demonstrate that learning-based quantizers at the relays can harness input correlations by operating independently yet collaboratively, enabling effective distributed compression in line with Berger-Tung-style coding. Results in both relay channel and diamond relay channel show that the proposed scheme, trained end-to-end with finite-order modulation, operates close to the theoretical bounds, given in Fig. 5 [3].

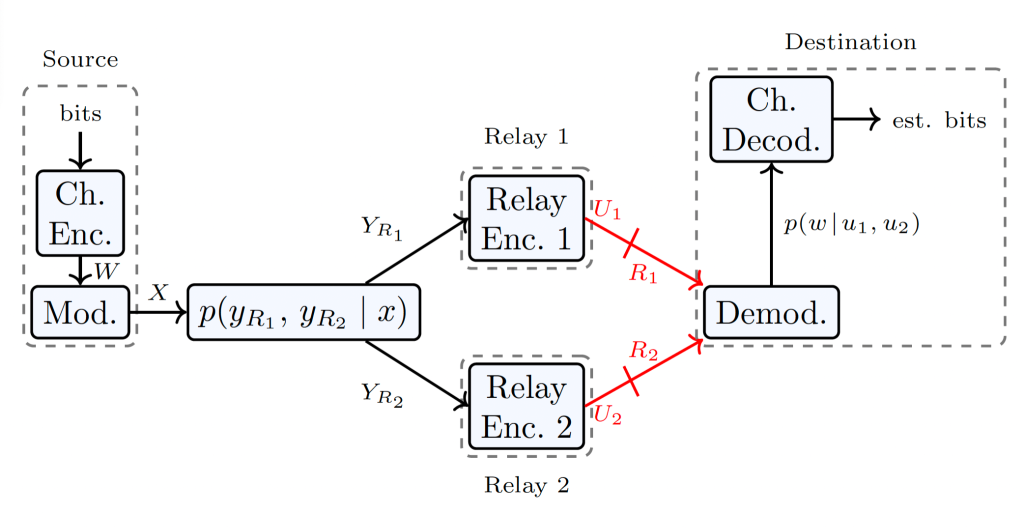
Fig. 4: Primitive diamond relay channel model. Red links indicate orthogonal (or out-of-band) relaying between the two relays and the destination.

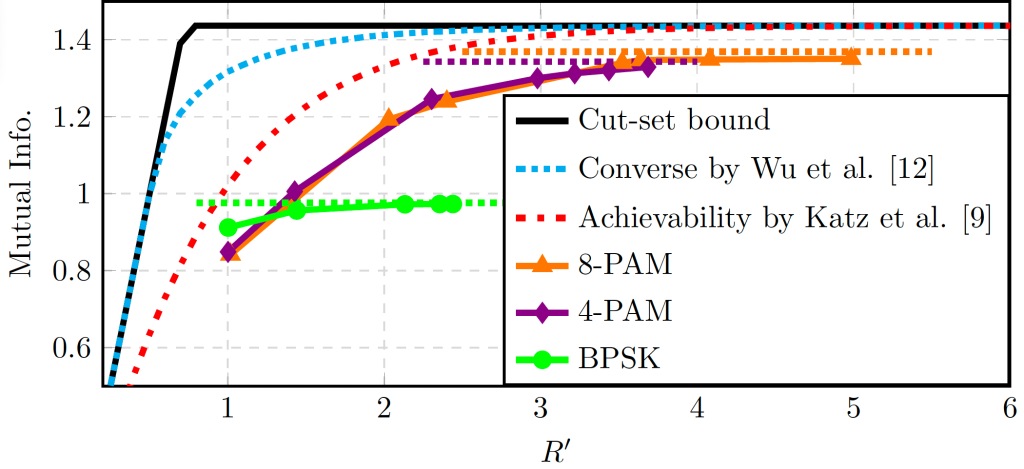
Fig. 5: Mutual information for the distributed scheme of the DRC under BPSK, 4-PAM, and 8-PAM modulations with γR1 = γR2 = 5 dB. Solid lines represent theoretical bounds where rates from both relays are chosen as R1 = R2 = R′. Dashed lines represent performance of two perfect relays (i.e., R1 → ∞, R2 → ∞) for the respective curves.